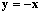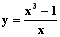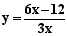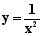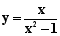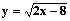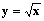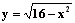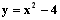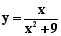SIMMETRIE ( seconda serie)
Prof. Mauro La Barbera
Determinare le eventuali simmetrie
SIMMETRIE DI UNA FUNZIONE
Se il grafico della curva presenta una simmetria rispetto all’asse delle ordinate allora la funzione si definisce pari.
Invece una funzione si dice dispari quando è simmetrica rispetto all’origine degli assi cartesiani.
- è simmetrica rispetto all'asse delle ascisse
- è simmetrica rispetto all'asse delle ordinate
- è simmetrica rispetto all'origine degli assi cartesiani
- non è simmetrica
- è simmetrica rispetto all'asse delle ascisse
- è simmetrica rispetto all'asse delle ordinate
- è simmetrica rispetto all'origine degli assi cartesiani
- non è simmetrica
- è simmetrica rispetto all'asse delle ascisse
- è simmetrica rispetto all'asse delle ordinate
- è simmetrica rispetto all'origine degli assi cartesiani
- non è simmetrica
- è simmetrica rispetto all'asse delle ascisse
- è simmetrica rispetto all'asse delle ordinate
- è simmetrica rispetto all'origine degli assi cartesiani
- non è simmetrica
- è simmetrica rispetto all'asse delle ascisse
- è simmetrica rispetto all'asse delle ordinate
- è simmetrica rispetto all'origine degli assi cartesiani
- non è simmetrica
- è simmetrica rispetto all'asse delle ordinate
- è simmetrica rispetto all'asse delle ascisse
- è simmetrica rispetto all'origine degli assi cartesiani
- non è simmetrica
- è simmetrica rispetto all'asse delle ordinate
- è simmetrica rispetto all'origine degli assi cartesiani
- non è simmetrica
- è simmetrica rispetto all'asse delle ascisse
- è simmetrica rispetto all'asse delle ordinate
- è simmetrica rispetto all'origine degli assi cartesiani
- non è simmetrica
- è simmetrica rispetto all'asse delle ascisse
- è simmetrica rispetto all'asse delle ordinate
- è simmetrica rispetto all'asse delle ascisse
- non è simmetrica
- è simmetrica rispetto all'origine degli assi cartesiani
- è simmetrica rispetto all'asse delle ordinate
- è simmetrica rispetto all'asse delle ascisse
- non è simmetrica
- è simmetrica rispetto all'origine degli assi cartesiani